从21点赌局到金融市场交易.
众所周知,赌博与交易有很多相似的性质与规则,而赌博相对于金融市场交易有着更加古老的历史,在漫漫历史长河中有一位天赋异禀的奇才,一度打破了赌场庄家对赌客的有利优势,这个人就是著名的MIT教授——爱德华·索普。
我们先简单介绍一下21点游戏的规则,由2到6人玩,使用除大小王之外的52张牌型,游戏的目标是使手中牌的点数之和不超过21点且尽量大。牌2~9分别记作 2~9点,10、J、Q、K记作10点,A视情况记作 1或11点。 谁总数大谁获胜,但总数超过21点则为 “爆牌” 直接失败,总数相同为平局。一张A带一张10点的牌为黑杰克,如果赌客玩家获得黑杰克可以赢得所下赌注的1.5倍。赌场担任庄家,与其余的赌客玩家对战,首回合,玩家与庄家各获得两张初始牌,一张翻开一张合上。随后玩家可以选择:拿一张牌(Hit)或结束拿牌(Stand),也可选择赌注翻倍并拿牌(Double)。如两张初始牌相同,可将它们分开,另压一份赌注,再补充至两张(Split)。等所有玩家结束拿牌后, 庄家看牌,若大于等于17点则不拿牌,反之拿牌直至17点, 爆牌则所有玩家获胜。
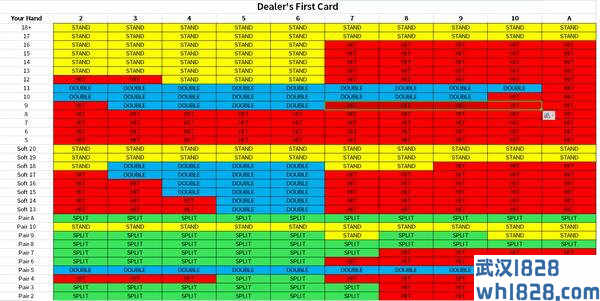
起初人们利用算取概率的方法来制定玩家的基本最优决策,这里我们省去繁琐的数学证明,用表格直观的显示各种情况下的最优决策。以下显示了不同情况下的庄家与玩家牌型,玩家应该选择的决策:
基本最优决策可以使得玩家在赌局中不那么劣势,但也没有使玩家获得明显优势。索普在此基础上进行改进后便在赌场中大展身手。其使用的方法是一种计牌客的计牌法,虽然赌场上流传着“扑克牌没有记忆”,但在赌场的21点游戏中,牌是有记忆的!因为上一轮用过的牌将不会出现在剩余的牌中,直到牌全部用完,用掉的牌才会重新洗牌,继续游戏。这将导致一副牌的组成在玩的过程中变化,优势在玩家与庄家之间切换。索普巧妙地利用了这一点,随着游戏进行,后续的牌依次从越来越少的剩余牌堆中出现时,就可以计算出何时会出现对玩家有利的机会,索普在每当他有优势时下大注,而在庄家有优势时下小注,最终总体上赚钱。索普用此思想设计了一个后来著名的计10点的制胜策略,并亲自在内华达的赌场实际测试策略结果,测试表现与预期一致,赚取颇丰。值得注意的是,索普会选择那些规则总体对玩家更公平的赌场,并尽量的单独包桌进行游戏。后来的团队作战更加发挥了索普思想的威力,这在电影《决胜21点》中表现的淋漓尽致。再之后,索普更是将著名的凯利公式运用到21点的赌局中来解决下注多少的问题。在被各大赌场拉黑,及21点的游戏规则发生改变后,索普开始转战全球最大赌场:华尔街股票市场。
索普转战股票市场后也是玩的风生水起,我想这和他早在21点的赌局中熟练发现胜算优势与掌握下注比例的技巧有关,而在金融市场交易中,最可利用的索普思想精髓便是在优势大的时候下大注这一思路,量化交易中的很多套路都可以回溯到这一根本性思想,如高频算法中的“冰山算法”,即有的交易所会把冰山订单用两个参数表示,V表示订单总量,p表示公开显示的量。我们可以对V和p建立概率模型,即计算一个给定的(V,p)值组合出现的概率,通过对历史数据的统计估算我们会得到一个概率密度函数,根据函数的概率分布来参考制定相应的交易策略。在此我们不详细介绍各种数学模型来估算交易中概率优势的例子,我们以普通交易者的方式来体会一下利用索普的思路解决日常交易中何为有利胜算的方法。特别强调,在交易中的有利胜算或某种规律是基于统计上的,并非真实的因果联系。
基于在掌握有利胜算时才主动冒风险下注的思想,普通交易者需要制定一个判断有利胜算的方针,例如,我是根据市场走势的空间与时间的统计分布,来判断每一笔交易的胜算。这种方法是一种利用市场走势的平均寿命框架来衡量风险与回报,即我们若是做国内期货周内交易,可以利用当前市场价格数据统计出每周内市场的走势幅度与持续时间长度的综合概率分布,如统计结果显示有68%的多头市场的涨幅介于价格的2%到4%之间,而持续时间介于2到3天,当天周一开盘市场价格就上涨4%多,那此时追多显然不是一个明智的交易决策;同理反之亦然。虽然我们无法明确判断市场价格的走势,但是运用统计方法可以凸显风险-回报分析的重要性,以至于我们不用主动参与到一个“老化”的市场中去。同样我们为了在长期安全的情况下最大化利润,可以采用例如固定风险百分比下注策略来取代21点中的凯利公式而运用到交易中去发挥作用。
从21点赌局游戏到金融市场交易,两者有很多共通之处,不论作为一个明智的赌客还是一个精明的交易者,都应在强调风险的情况下,当掌握有利胜算时,才主动承担风险以博取潜在的收益,这是索普大神给所有交易者留下的精神财富。













发表评论